Пять интересных задач в редакцию "Дни.ру" прислала педагог по математике Wunderpark International School Анастасия Годунова.
Задача №1
У Маши не хватало для покупки букваря семи копеек, а у Миши одной копейки. Они сложились, чтобы купить один букварь на двоих, но денег все равно не хватило. Сколько стоил букварь?
Во многих задачах и взрослые, и дети отбрасывают варианты типа "не было совсем", "было равно нулю". И именно на этом построены задачи, типа №1.
Ответ: Букварь стоил 7 копеек.
Задача №2
Однажды Петр Петрович сказал: "День, когда послезавтра станет вчера, будет также далек от воскресенья, как и тот день, когда позавчера было завтра. В какой день недели он это сказал?
Эта задача легко решается, если изобразить дни недели в круг или каким-то иным способом отобразить их цикличную смену. После призвать на помощь симметрию и ответ очевиден.
Ответ: Воскресенье.
Задача №3
Шесть гномиков построили себе шесть домиков и проложили прямые не пересекающиеся дорожки так, чтобы к каждому домику подходило четыре дорожки. Нарисуйте это.
Эта задачка почти никогда не решается сразу, если вы не знаете ответа. Зато ее можно раскрутить методом последовательного улучшения. Отбросьте сначала условие на непересекаемость или на прямоту линий. Составьте решение и улучшайте, пока не будут соблюдены все условия.
Ответ:
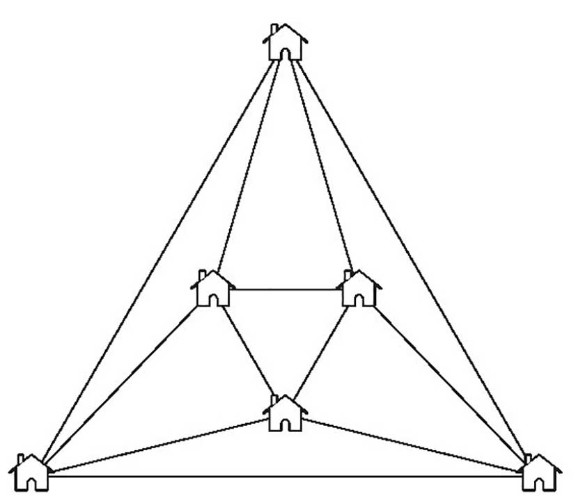
Задача №4
Разрежьте треугольник тремя отрезками на четыре треугольника так, чтобы каждый треугольник, граничил с тремя другими.
Эта задача по принципу решения похожа на предыдущую разрезайте на треугольник на четыре и наблюдайте, как нужно изменить расположение отрезков, чтобы выполнялось условие задачи. Если возьмете правильный треугольник (у которого все стороны равны), то решение будет еще и симметричным относительно центра треугольника.
Ответ:
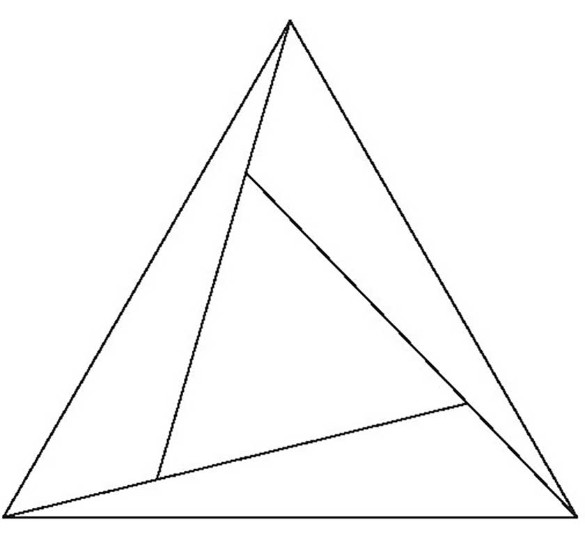
Задача №5
Имеется 26 монет. Одна из них фальшивая. Она легче по весу, чем настоящие монеты. Имеются чашечные весы. Как всего лишь за три взвешивания найти фальшивую монету?
Практически во всех задачах на взвешивание секрет состоит в делении общего количества на три, а не на две кучки. А вот на какие Вам предстоит догадаться.
Ответ: Первое взвешивание 9 и 9 монет, отложено 8 (26 = 9+9+8). Если одна из кучек в 9 монет оказывается легче, значит фальшивая монета в ней. Если обе кучки равны по весу, значит фальшивая монета там, где 8 монет.
Соответственно, второе взвешивание: 3 и 3 монеты. Отложено 3 или 2 (9=3+3+3, 8=3+3+2)
Третье взвешивание: 3= 1+1+1 или 2=1+1









